Least Common Multiple (LCM) Calculator

Calculate square roots, cube roots, and more.

LCM Result

LCM of given positive numbers will be displayed here!

0
Calculation Steps
HCF Calculator

Least Common Multiple

A comprehensive guide about Least Common Multiple (LCM)

What is LCM?

The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by each of the given numbers without leaving a remainder. LCM is a fundamental concept in number theory and is often used in problems involving fractions, ratios, and scheduling (e.g., finding when events that occur at different intervals will happen simultaneously).

For example, the LCM of 4 and 6 is 12 because 12 is the smallest number that both 4 and 6 can divide evenly (4 × 3 = 12, 6 × 2 = 12).

Types of Ways to Find LCM

There are several methods to calculate the LCM of two or more numbers. Here, we’ll explore two common approaches: the Prime Factorization Method and the Division Method (also known as the ladder method).

1
Prime Factorization Method

In this method, we break down each number into its prime factors, then take the highest power of each prime that appears in the factorizations and multiply them to get the LCM.

Steps to Calculate LCM By Prime Factorization

Responsive image
Example: Find the LCM of 12 and 18.
1
Prime factorization of 12: 12 = 2 × 2 × 3 = 2² × 3¹.
2
Prime factorization of 18: 18 = 2 × 3 × 3 = 2¹ × 3².
3
Highest powers: 2² (from 12) and 3² (from 18).
4
LCM = 2² × 3² = 4 × 9 = 36.
5
Your calculation will be saved in the history section below.

2
Division Method (Ladder Method)

In the division method, we divide the numbers by their common prime factors step-by-step until no further division is possible, then multiply all the divisors to find the LCM.

Steps to Calculate LCM By Division Method

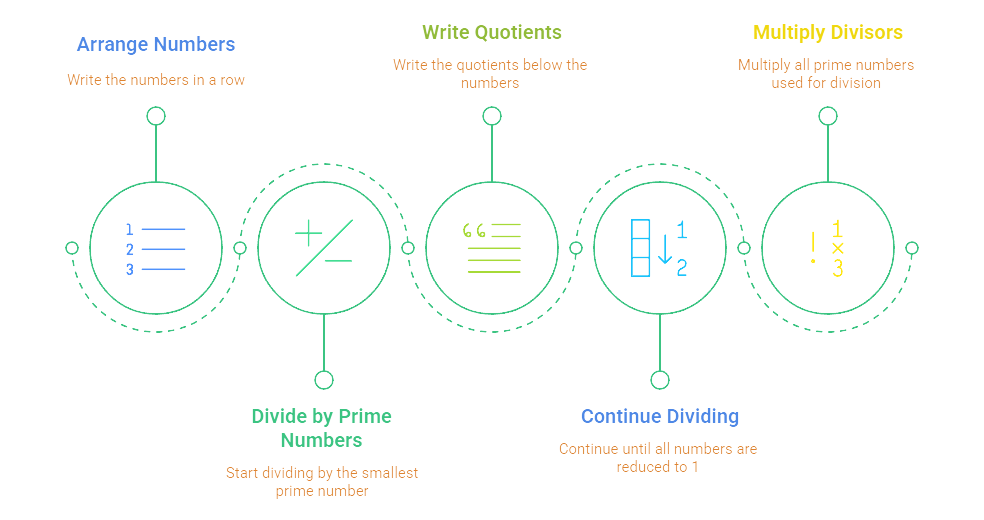
Responsive image
Example: Find the LCM of 12 and 18.
1
Start with 12, 18.
2
Divide by 2: 12 ÷ 2 = 6, 18 ÷ 2 = 9 → (6, 9).
3
3.Divide by 3: 6 ÷ 3 = 2, 9 ÷ 3 = 3 → (2, 3).
4
No common factors left
5
Multiply divisors: 2 × 3 × 2 × 3 = 36.
6
LCM = 36.
Pro Tip

Click the Clear button to start the calculation from starting and all the fields including result, calculation steps will be reset.

Frequently Asked Questions (FAQ)

Can LCM be calculated for more than two numbers?

Yes, LCM can be calculated for any number of integers. Both methods (Prime Factorization and Division) can be extended to handle multiple numbers by applying the same logic iteratively.

What is the relationship between LCM and GCD?

For two numbers \(a\) and \(b\), the product of their LCM and GCD (Greatest Common Divisor) equals the product of the numbers: LCM(a, b) × GCD(a, b) = a × b.

What if one of the numbers is 0?

The LCM of 0 and any number is undefined in the context of positive integers because 0 does not have a meaningful set of multiples in this sense.

Which method is faster for large numbers?

The Division Method is often faster for larger numbers because it avoids the need to fully factorize each number into primes, especially if the numbers share many common factors.